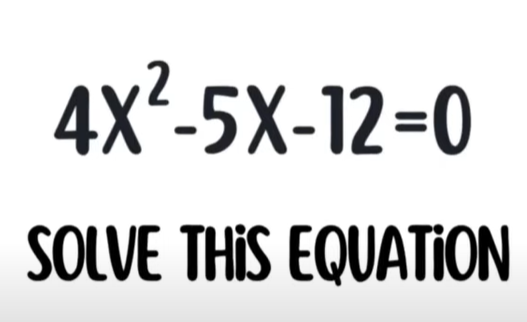Table of Contents
The quadratic equation holds immense significance in mathematics, serving various purposes, and you will come across it frequently throughout your educational journey. Consider in detail how to solve the equation 4x ^ 2 – 5x – 12 = 0
Standard Form
The standard form of a quadratic equation is:
ax^2 + bx + c = 0, where a, b, and c are real numbers. The solutions to this equation are called roots. The x-intercepts (where y = 0) are given by:
x_1 = -b/2a and
x_2 = -b/4a
Hidden Quadratic Equations!
The quadratic formula stands as a potent tool in solving quadratic equations, offering a method to determine solutions for any such equation. However, its utilization may pose challenges due to its complexity.
Let’s start by taking an example:
4x ^ 2 – 5x – 12 = 0
About the Quadratic Formula
A quadratic equation is an equation of the form x^2 + bx + c = 0. The quadratic formula can be used to find the roots of a quadratic equation, which are solutions to an equation that satisfy both sides of that equation. The discriminant b^2 – 4ac is used to determine whether or not there will be unique real solutions (roots).
Discriminant
The discriminant is the b2-4ac. If it’s positive, there are two real solutions; if it’s negative, there are no real solutions, only complex ones.

Using the Quadratic Formula
The quadratic formula is a way of finding the roots (x-intercepts) of a quadratic equation in one variable. It can also be used to determine whether or not an equation has any real solutions, or if it’s purely imaginary.
To find the roots of an equation using the quadratic formula, first write down what you know about your equation:
The leading coefficient (a number multiplied by itself) is 1
The degree (or power) of x is 2
Step-by-Step Solution – 4x ^ 2 – 5x – 12 = 0
A quadratic equation with a positive discriminant has infinitely many solutions. A quadratic equation with a zero discriminant (or no real roots) has only two real solutions. A quadratic equation with a negative discriminant has no real roots at all!
A quadratic equation with a negative discriminant has no real solutions at all!
The discriminant is the only thing you need to know about the roots of a quadratic equation in order to find them. If it’s positive, there are two real solutions. If it’s zero, there are two complex solutions (this means that there are two sets of complex numbers that solve the equation).Step 1: Identify the coefficients: In our equation, 4 is the coefficient of x^2, -5 is the coefficient of x, and -12 is the constant term.
Step 2: Utilize the Quadratic Formula: It is the prevailing approach for solving quadratic equations. It is expressed as follows:
x = (-b ± √(b^2 – 4ac)) / 2a
Step 3: Substitute the coefficients into the formula: For our equation 4x^2 – 5x – 12 = 0, we have:
a = 4 b = -5 c = -12
Step 4: Calculate the discriminant (b^2 – 4ac): The discriminant helps determine the nature of the roots. If the discriminant is positive, there are two distinct real roots; if it’s zero, there’s one real root; and if it’s negative, there are two complex roots.
b^2 – 4ac = (-5)^2 – 4 4 (-12) b^2 – 4ac = 25 + 192 b^2 – 4ac = 217
Step 5: Find the roots: Now, apply the quadratic formula with the discriminant value:
x = (-(-5) ± √217) / 2 * 4
x = (5 ± √217) / 8
Therefore, the two roots are:
x = (5 + √217) / 8 x = (5 – √217) / 8
After following the step-by-step process, we have successfully solved the quadratic equation 4x ^ 2 – 5x – 12 = 0. The two roots obtained are (5 + √217) / 8 and (5 – √217) / 8. These values correspond to the x-coordinates where the equation intersects the x-axis. The process of solving quadratic equations holds fundamental importance in mathematics and finds significant applications across diverse fields like physics, engineering, finance.